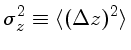
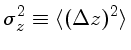
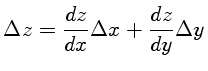
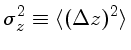 |
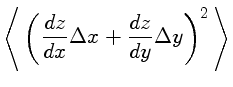 |
||
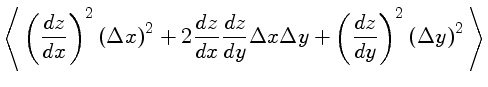 |
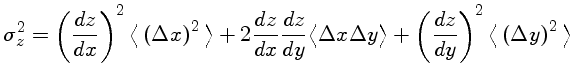
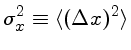
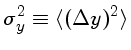
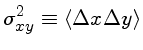
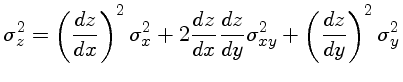
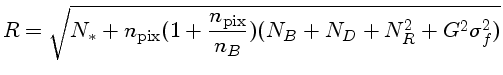
| número total de contagens coletadas do objeto (em elétrons) | |
|
|
número de pixels considerados |
| número de pixeis de fundo (céu) | |
| número total de contagens por pixel de fundo (céu, em elétrons) | |
| número total de contagens por pixel de corrente de escuro (térmicos, em elétrons) | |
| ruído de leitura por pixel (em elétrons) | |
| Ganho do detector (número de elétrons/ADU) | |
Mas quando convertemos estas contagens em magnitudes observadas em um certo filtro, representado pelo seu comprimento de onda efetivo, temos outras incertezas:
Neste caso, como
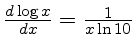
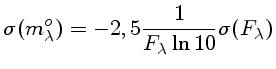
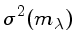 |
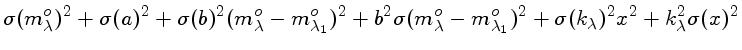 |
||
![]()