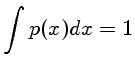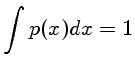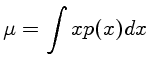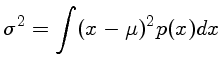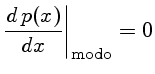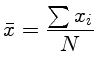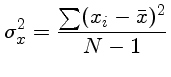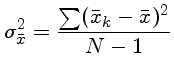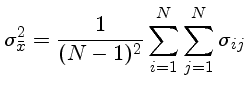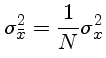Variança da média
Definimos como 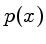 a probabilidade de um evento ocorrer entre
a probabilidade de um evento ocorrer entre
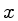 e
e 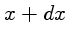 :
a média μ
a variança
:
a média μ
a variança 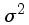 :
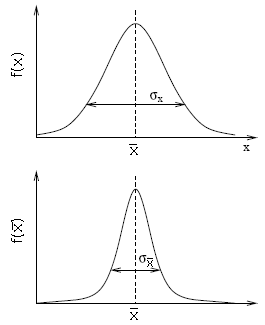
o desvio padrão
:
o desvio padrão 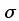 , e o modo, que é o valor mais provável
da distribuição
Definindo a média de um conjunto de medidas,
, e o modo, que é o valor mais provável
da distribuição
Definindo a média de um conjunto de medidas, 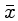 :
e a variança do conjunto:
Como nossas medidas são finitas, a média
:
e a variança do conjunto:
Como nossas medidas são finitas, a média 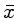 não é idêntica à
média μ.
Se medirmos nossas médias
não é idêntica à
média μ.
Se medirmos nossas médias 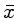 várias vezes, podemos calcular
a variança da média:
Substituindo a definição da média
várias vezes, podemos calcular
a variança da média:
Substituindo a definição da média 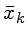 , obtemos
Se as medidas i e j não são correlacionadas,
, obtemos
Se as medidas i e j não são correlacionadas,
 Volta: Mínimos Quadrados
Astronomia e Astrofisica
©Kepler de Souza Oliveira Filho
Volta: Mínimos Quadrados
Astronomia e Astrofisica
©Kepler de Souza Oliveira Filho
Modificada em 22 de set de 2009