




Próxima: Schwarzschild
Volta: Interiores Estelares
Anterior: Novas e Supernovas
 Para campos gravitacionais fortes, como no caso de estrelas de nêutrons
e buracos negros, precisamos utilizar a
equação de campo de Albert Einstein (1879-1955),
já que a massa e energia curvam a geometria do espaço-tempo.
Como esta equação precisa ser descrita por
análise tensorial, vamos primeiro fazer uma
revisão de coordenadas.
Para campos gravitacionais fortes, como no caso de estrelas de nêutrons
e buracos negros, precisamos utilizar a
equação de campo de Albert Einstein (1879-1955),
já que a massa e energia curvam a geometria do espaço-tempo.
Como esta equação precisa ser descrita por
análise tensorial, vamos primeiro fazer uma
revisão de coordenadas.
 Um ponto no espaço-tempo pode ser caracterizado por um evento,
que aconteceu em um lugar do espaço, em um certo momento.
Podemos caracterizar o espaço-tempo, e as transformações
de Lorentz, propostas pelo físico holandês
Hendrik Antoon Lorentz (1853-1928) em 1904,
e utilizadas por Einstein na Teoria da Relatividade Especial em 1905:
Um ponto no espaço-tempo pode ser caracterizado por um evento,
que aconteceu em um lugar do espaço, em um certo momento.
Podemos caracterizar o espaço-tempo, e as transformações
de Lorentz, propostas pelo físico holandês
Hendrik Antoon Lorentz (1853-1928) em 1904,
e utilizadas por Einstein na Teoria da Relatividade Especial em 1905:
introduzindo a coordenada imaginária 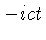 no lugar da coordenada temporal
no lugar da coordenada temporal 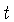 .
Desta maneira, para um
espaço cartesiano
[René Descartes (1596-1650)], temos:
Com estas definições, podemos transformar de um
sistema de coordenadas para outro mantendo a relação:
.
Desta maneira, para um
espaço cartesiano
[René Descartes (1596-1650)], temos:
Com estas definições, podemos transformar de um
sistema de coordenadas para outro mantendo a relação:
 Um sistema de coordenadas descrito pelas coordenadas
Um sistema de coordenadas descrito pelas coordenadas
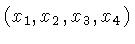 acima é chamado de um sistema de Minkowski,
pois foi proposto pelo matemático russo-alemão
Hermann Minkowski (1864-1909).
Este sistema é um espaço Euclidiano de quatro dimensões,
e a transformação de Lorentz corresponde a uma
rotação
neste espaço quadri-dimensional.
acima é chamado de um sistema de Minkowski,
pois foi proposto pelo matemático russo-alemão
Hermann Minkowski (1864-1909).
Este sistema é um espaço Euclidiano de quatro dimensões,
e a transformação de Lorentz corresponde a uma
rotação
neste espaço quadri-dimensional.
Em um sistema de coordenadas Euclidiano, a unidade de distância não
varia com a posição.
Carl Friedrich Gauss (1777-1855)
propôs um sistema de coordenadas geral, não Euclidiano;
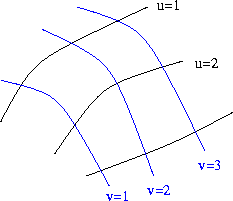
imaginemos um sistema de coordenadas de curvas arbitrárias,
não justapostas, em uma superfície qualquer.
Em uma direção designemos as curvas por 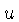 , designando-as
, designando-as
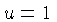 ,
, 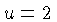 , .... Entre as curvas
, .... Entre as curvas 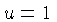 e
e 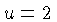 podemos imaginar
um número infinito de curvas, correspondendo aos números naturais
entre 1 e 2. As curvas não se intersectam e
somente uma curva passa por cada ponto da superfície,
de modo que um valor perfeitamente definido de
podemos imaginar
um número infinito de curvas, correspondendo aos números naturais
entre 1 e 2. As curvas não se intersectam e
somente uma curva passa por cada ponto da superfície,
de modo que um valor perfeitamente definido de 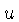 pode ser estabelecido
para cada ponto. Podemos estabelecer um sistema
pode ser estabelecido
para cada ponto. Podemos estabelecer um sistema 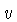 de coordenadas sobre a superfície, de modo que um valor
de
de coordenadas sobre a superfície, de modo que um valor
de 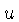 e
e 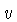 possam ser estabelecidos para cada ponto da superfície.
Chamamos estes pontos de coordenadas gaussianas da superfície.
Dois pontos próximos terão coordenadas
possam ser estabelecidos para cada ponto da superfície.
Chamamos estes pontos de coordenadas gaussianas da superfície.
Dois pontos próximos terão coordenadas 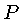 e
e 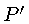 ,
com coordenadas:
onde
,
com coordenadas:
onde 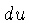 e
e 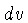 são pequenos. A distância entre estes pontos
são pequenos. A distância entre estes pontos
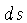 será dada por:
onde
será dada por:
onde 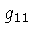 ,
, 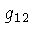 e
e 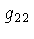 dependem de
dependem de 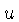 e
e 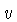 ,
e representam a variação da unidade de distância em
relação a elas. Somente para o caso especial em que a superfície
seja Euclidiana e as coordenadas cartesianas, isto é,
independentes, podemos escrever:
Podemos generalizar as coordenadas de Gauss para um contínuo
de três ou mais dimensões. Para um contínuo de quatro
dimensões, como o espaço de Minkowski, podemos escrever
que dois pontos adjacentes estão separados por uma distância
ds tal que:
onde os valores de
,
e representam a variação da unidade de distância em
relação a elas. Somente para o caso especial em que a superfície
seja Euclidiana e as coordenadas cartesianas, isto é,
independentes, podemos escrever:
Podemos generalizar as coordenadas de Gauss para um contínuo
de três ou mais dimensões. Para um contínuo de quatro
dimensões, como o espaço de Minkowski, podemos escrever
que dois pontos adjacentes estão separados por uma distância
ds tal que:
onde os valores de 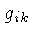 variam com a posição.
onde
está implícita a soma sobre todos os valores de i e k.
ds, a métrica, é um escalar e tem o mesmo valor em qualquer
sistema de coordenadas.
variam com a posição.
onde
está implícita a soma sobre todos os valores de i e k.
ds, a métrica, é um escalar e tem o mesmo valor em qualquer
sistema de coordenadas.
Por exemplo, para um sistema de coordenadas esféricas no espaço
plano:
enquanto em coordenadas cilíndricas:
Na relatividade geral, a velocidade da luz não é mais mantida
constante, mas depende do sistema de coordenadas quando um
campo gravitacional está presente. A idéia fundamental
da relatividade geral é que todos sistemas de coordenadas gaussianos
são equivalentes para a formulação das leis gerais da natureza,
de modo que as equações não devem mudar de forma ao
serem submetidas a substituições arbitrárias das
variáveis gaussianas. As transformações
de Lorentz não satisfazem esta condição.
A equação de campo de Einstein,
sem a constante cosmológica,
isto é, válida para distâncias menores que 100 Mpc:
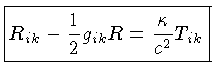 |
(1.89) |
onde 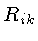 é o tensor espaço-tempo,
é o tensor espaço-tempo,
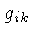 são as componentes do tensor métrico e dependem do
sistema de coordenadas usado e da unidade da coordenada temporal,
são as componentes do tensor métrico e dependem do
sistema de coordenadas usado e da unidade da coordenada temporal,
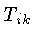 é o
tensor momentum-energia,
que depende da distribuição e movimento das
massas e do campo eletromagnético,
e
é a constante gravitacional de Einstein,
na verdade as equações de campo formam um sistema de 10 equações diferencias
de segunda ordem acopladas,
considerando as combinações dos quatro i e k.
O tensor métrico gik tem dez componentes, mas
as somente 6 das equações de campo são independentes. Os outros
4 graus de liberdade permitem que as 4 coordenadas do sistema de
coordenadas sejam escolhidas livremente.
A escolha dos sistema de coordenadas pode facilitar a solução das
equações de campo, mas a interpretação do sistema de coordenadas
torna-se importante e não trivial.
é o
tensor momentum-energia,
que depende da distribuição e movimento das
massas e do campo eletromagnético,
e
é a constante gravitacional de Einstein,
na verdade as equações de campo formam um sistema de 10 equações diferencias
de segunda ordem acopladas,
considerando as combinações dos quatro i e k.
O tensor métrico gik tem dez componentes, mas
as somente 6 das equações de campo são independentes. Os outros
4 graus de liberdade permitem que as 4 coordenadas do sistema de
coordenadas sejam escolhidas livremente.
A escolha dos sistema de coordenadas pode facilitar a solução das
equações de campo, mas a interpretação do sistema de coordenadas
torna-se importante e não trivial.
Os tensores podem ser dilatados ou comprimidos, girados e invertidos,
quando transformamos de um sistema de coordenadas para outro, mas não
podem ser deslocados (sem termos aditivos) ou sujeitos a
operações não lineares. Mas suas componentes podem, e geralmente são,
funções não lineares das coordenadas.
O tensor de segunda ordem
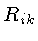 , que descreve a forma do espaço-tempo,
é chamado de tensor Ricci
[Georgorio Ricci-Curbastro (1853-1925)],
e contraído nos dá a curvatura escalar do espaço-tempo:
, que descreve a forma do espaço-tempo,
é chamado de tensor Ricci
[Georgorio Ricci-Curbastro (1853-1925)],
e contraído nos dá a curvatura escalar do espaço-tempo:
também chamada de curvatura de Riemann
[Georg Friedrich Bernhard Riemann (1826-1866)].
Na equação (1.89), os dois índices
i e k variam de 0 a 3, os
dois termos à esquerda do sinal de igualdade representam
a curvatura do espaço-tempo e
o termo à direita as forças que atuam neste sistema.
Os índices repetidos significam soma,
pela convenção da soma de Einstein.
O tensor de Ricci tem 44=256 componentes no espaço-tempo
quadrimensional, mas não todas são independentes.
A equação é escrita de forma tensorial de modo a não depender
dos detalhes do sistema de coordenadas, já que sempre podemos
transformar o sistema de coordenadas para qualquer outro.
Na relatividade geral não existe sistema de coordenadas
absoluto e a única forma de medir o movimento de um corpo
é em relação a outro objeto.
O tensor de segunda ordem de Ricci é função
da geodésica:
através dos
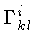 ,
os símbolos de Christoffel
[Elwin Bruno Christoffel (1829-1900)]:
Os símbolos de Christoffel não são tensores.
Para um sistema cartesiano em um plano, todos os gij
são constantes e todas as derivadas do tensor métrico são nulas,
de modo que todos os símbolos de Christoffel são nulos.
,
os símbolos de Christoffel
[Elwin Bruno Christoffel (1829-1900)]:
Os símbolos de Christoffel não são tensores.
Para um sistema cartesiano em um plano, todos os gij
são constantes e todas as derivadas do tensor métrico são nulas,
de modo que todos os símbolos de Christoffel são nulos.
O tensor de curvatura de Einstein
é definido como:
Para um gás, o tensor energia-momentum em coordenadas curvilíneas
pode ser escrito como:
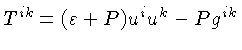 |
(1.90) |
onde
é a densidade de energia da matéria, incluindo a energia de repouso,
medida no sistema em repouso com a matéria,
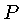 é a pressão isotrópica,
ui
é a quadri-velocidade do gás e
ds o intervalo entre dois pontos xi
e xi+dxi.
é a pressão isotrópica,
ui
é a quadri-velocidade do gás e
ds o intervalo entre dois pontos xi
e xi+dxi.
Como a quadri-velocidade de um fluido medido por um observador
em co-movimento com o fluido é simplesmente ui=(1,0,0,0),
temos para um gás ideal:
O tensor energia-momentum
para um campo eletromagnético é dado por
onde 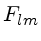 é o tensor de campo eletromagnético. Este tensor
causa uma tensão
é o tensor de campo eletromagnético. Este tensor
causa uma tensão
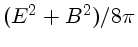 ao longo das linhas de campo,
e uma pressão
ao longo das linhas de campo,
e uma pressão
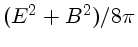 perpendicular às das linhas de campo,
onde
perpendicular às das linhas de campo,
onde
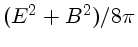 é a densidade de energia do campo eletromagnético.
é a densidade de energia do campo eletromagnético.
Na relatividade especial, isto é, para campos
gravitacionais desprezáveis, o intervalo de tempo próprio 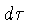 entre dois eventos definidos pelas coordenadas
entre dois eventos definidos pelas coordenadas
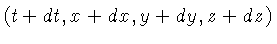 e
e 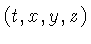 é dado pela equação:
é dado pela equação:
onde 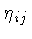 é a métrica de Minkowiski, equivalente a
é a métrica de Minkowiski, equivalente a
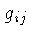 na métrica generalizada.
Mas para um campo gravitacional forte, o intervalo invariante de Riemann
(tem o mesmo valor em qualquer sistema de coordenadas)
na métrica generalizada.
Mas para um campo gravitacional forte, o intervalo invariante de Riemann
(tem o mesmo valor em qualquer sistema de coordenadas)
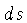 é dado por:
onde
é dado por:
onde 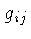 é um tensor simétrico, chamado de tensor métrico.
Para pequenas regiões do espaço-tempo, o espaço pode
ser considerado plano e as coordenadas Lorentzianas
[Hendrik Antoon Lorentz (1853-1928)]. Neste caso,
Um postulado da geometria de Riemann é que, em volta de qualquer
ponto não singular, é possível definir um sistema de
coordenadas em que o espaço é localmente inercial. Na
relatividade geral este postulado é chamado de
princípio da equivalência
e significa que, na vizinhança de um ponto
não singular arbitrário, o campo gravitacional é
equivalente a uma aceleração uniforme.
é um tensor simétrico, chamado de tensor métrico.
Para pequenas regiões do espaço-tempo, o espaço pode
ser considerado plano e as coordenadas Lorentzianas
[Hendrik Antoon Lorentz (1853-1928)]. Neste caso,
Um postulado da geometria de Riemann é que, em volta de qualquer
ponto não singular, é possível definir um sistema de
coordenadas em que o espaço é localmente inercial. Na
relatividade geral este postulado é chamado de
princípio da equivalência
e significa que, na vizinhança de um ponto
não singular arbitrário, o campo gravitacional é
equivalente a uma aceleração uniforme.
A conservação de energia-momentum é expressa,
por construção, pela lei fundamental de geometria:
onde
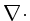 denota a divergência covariante, com componentes:
com o determinante
denota a divergência covariante, com componentes:
com o determinante
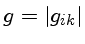 .
.
A equação de campo de Einstein (1.89):
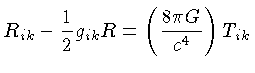 |
(1.91) |
precisa ser resolvida para
dar a equação
da geodésica (world line) de
uma partícula, isto é, a distância
entre dois eventos, definida
em termos do seu tempo próprio 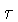 e da sua quadri-velocidade
e da sua quadri-velocidade 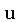 como um extremo:
como um extremo:
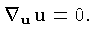 |
(1.92) |
A densidade de massa-energia, medida por um observador de
quadri-velocidade 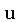 é dada por:
A equação tensorial (1.89), no limite de campos
gravitacionais fracos e velocidades não relativísticas,
se reduz à equação de Poisson (1.111).
é dada por:
A equação tensorial (1.89), no limite de campos
gravitacionais fracos e velocidades não relativísticas,
se reduz à equação de Poisson (1.111).
O movimento de uma partícula viajando de 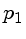 a
a 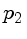 no espaço-tempo é o caminho para o qual o tempo próprio dado por
no espaço-tempo é o caminho para o qual o tempo próprio dado por
é um extremo, onde
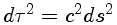 .
.
Aplicando o cálculo variacional para achar o extremo:
onde o Lagrangiano é definido por:
e
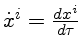 .
O Lagrangiano se parece com energia cinética - não existe energia potencial
nesta formulação, pois esta é representada pela curvatura do espaço-tempo.
.
O Lagrangiano se parece com energia cinética - não existe energia potencial
nesta formulação, pois esta é representada pela curvatura do espaço-tempo.
Na relatividade geral, as trajetórias dos fótons têm ds=0
e 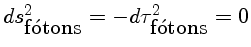 ,
onde
,
onde 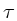 é o tempo próprio,
isto é, medido no referencial da partícula.
é o tempo próprio,
isto é, medido no referencial da partícula.
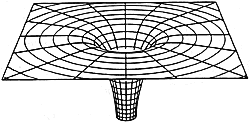 A equação de campo de Einstein vale para qualquer sistema
de coordenadas generalizadas. Porque não escolhemos as
coordenadas esféricas normais? Porque estas coordenadas
não incluem a curvatura do espaço. Precisamos modificá-la
para incluir a curvatura causada pelos efeitos gravitacionais,
mas preservando a simetria esférica.
A equação de campo de Einstein vale para qualquer sistema
de coordenadas generalizadas. Porque não escolhemos as
coordenadas esféricas normais? Porque estas coordenadas
não incluem a curvatura do espaço. Precisamos modificá-la
para incluir a curvatura causada pelos efeitos gravitacionais,
mas preservando a simetria esférica.
Em coordenadas esféricas
(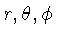 ),
a distância entre dois eventos é dada de forma genérica por:
),
a distância entre dois eventos é dada de forma genérica por:
onde 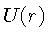 ,
, 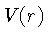 e
e 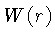 são funções de
são funções de 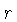 .
.
Encontrar a solução da equação de campo de
Einstein significa encontrar a geodésica que descreve
o intervalo entre os eventos, para dados valores do tensor
momentum-energia.
Sem perda de generalidade, podemos escolher as funções 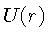 e
e 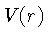 , com
, com 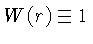 ,
escrevendo:
,
escrevendo:
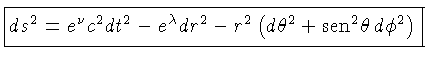 |
(1.93) |
onde
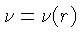 e
e
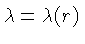 são as funções que
queremos determinar. Esta forma foi utilizada por
Karl Schwarzschild (1873-1916) em 1916, bem como por
Richard Chase Tolman (1881-1948)
no seu artigo publicado em 1939 no Physical Review, 55, p. 364-373,
e
Julius Robert Oppenheimer (1904-1967) &
George Michael Volkoff (1914-2000)
no artigo publicado no mesmo volume, p. 374-381.
são as funções que
queremos determinar. Esta forma foi utilizada por
Karl Schwarzschild (1873-1916) em 1916, bem como por
Richard Chase Tolman (1881-1948)
no seu artigo publicado em 1939 no Physical Review, 55, p. 364-373,
e
Julius Robert Oppenheimer (1904-1967) &
George Michael Volkoff (1914-2000)
no artigo publicado no mesmo volume, p. 374-381.
Trata-se de uma métrica estática
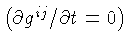 e ortogonal
e ortogonal
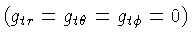 .
O elemento espacial de distância é dado por
.
O elemento espacial de distância é dado por
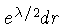 .
.
As únicas componentes covariantes não nulas do tensor métrico
para esta métrica de Schwarzschild
com 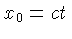 são:
são:
e os símbolos de Christoffel:
se reduzem a:
o tensor de Ricci:
e finalmente a curvatura de Riemann:
 Astronomia e Astrofísica
Astronomia e Astrofísica






Próxima: Covariante e Contravariante
Próxima: Schwarzschild
Volta: Interiores Estelares
Anterior: Novas e Supernovas
©
Modificada em 9 out 2011
 Um ponto no espaço-tempo pode ser caracterizado por um evento,
que aconteceu em um lugar do espaço, em um certo momento.
Podemos caracterizar o espaço-tempo, e as transformações
de Lorentz, propostas pelo físico holandês
Hendrik Antoon Lorentz (1853-1928) em 1904,
e utilizadas por Einstein na Teoria da Relatividade Especial em 1905:
Um ponto no espaço-tempo pode ser caracterizado por um evento,
que aconteceu em um lugar do espaço, em um certo momento.
Podemos caracterizar o espaço-tempo, e as transformações
de Lorentz, propostas pelo físico holandês
Hendrik Antoon Lorentz (1853-1928) em 1904,
e utilizadas por Einstein na Teoria da Relatividade Especial em 1905:
 Para campos gravitacionais fortes, como no caso de estrelas de nêutrons
e buracos negros, precisamos utilizar a
equação de campo de Albert Einstein (1879-1955),
já que a massa e energia curvam a geometria do espaço-tempo.
Como esta equação precisa ser descrita por
análise tensorial, vamos primeiro fazer uma
revisão de coordenadas.
Para campos gravitacionais fortes, como no caso de estrelas de nêutrons
e buracos negros, precisamos utilizar a
equação de campo de Albert Einstein (1879-1955),
já que a massa e energia curvam a geometria do espaço-tempo.
Como esta equação precisa ser descrita por
análise tensorial, vamos primeiro fazer uma
revisão de coordenadas.
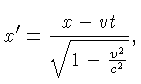
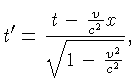
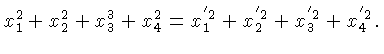
 Um sistema de coordenadas descrito pelas coordenadas
Um sistema de coordenadas descrito pelas coordenadas
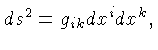
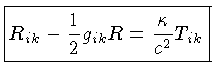
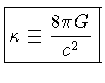
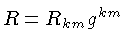
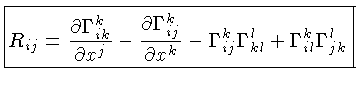
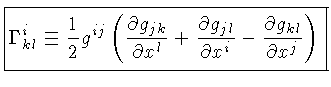
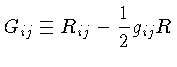
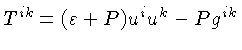
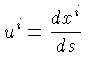
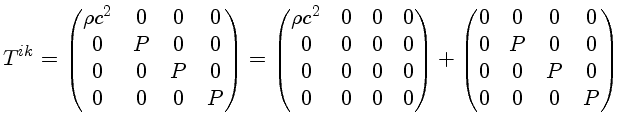
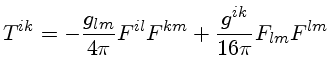
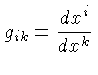
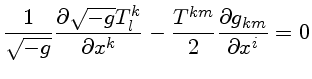
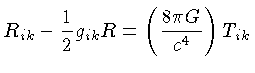
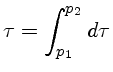

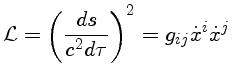
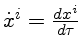 .
O Lagrangiano se parece com energia cinética - não existe energia potencial
nesta formulação, pois esta é representada pela curvatura do espaço-tempo.
.
O Lagrangiano se parece com energia cinética - não existe energia potencial
nesta formulação, pois esta é representada pela curvatura do espaço-tempo.
 A equação de campo de Einstein vale para qualquer sistema
de coordenadas generalizadas. Porque não escolhemos as
coordenadas esféricas normais? Porque estas coordenadas
não incluem a curvatura do espaço. Precisamos modificá-la
para incluir a curvatura causada pelos efeitos gravitacionais,
mas preservando a simetria esférica.
A equação de campo de Einstein vale para qualquer sistema
de coordenadas generalizadas. Porque não escolhemos as
coordenadas esféricas normais? Porque estas coordenadas
não incluem a curvatura do espaço. Precisamos modificá-la
para incluir a curvatura causada pelos efeitos gravitacionais,
mas preservando a simetria esférica.
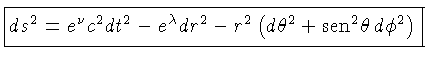
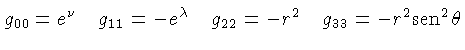
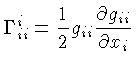
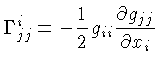
![$ \Gamma^i_{ij} = \frac{1}{2}g_{ii} [\frac{\partial g_{ii}}{\partial x_j}+ \frac{\partial g_{jj}}{\partial x_i}]$](img3018.gif)
![$ \Gamma^i_{ji} = \frac{1}{2}g_{ii} [\frac{\partial g_{ii}}{\partial x_i}+ \frac{\partial g_{ii}}{\partial x_j}]$](img3019.gif)
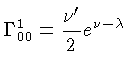
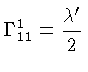
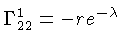


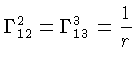
![$ R_{00} = [-\frac{\nu^{\prime\prime}}{2} +
\frac{\lambda^\prime... \frac{(\nu^\prime)^2}{4} -
\frac{\nu^\prime}{r}]e^{(\nu-\lambda)}$](img3028.gif)
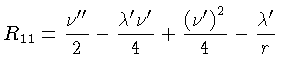
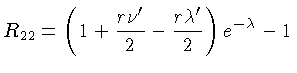
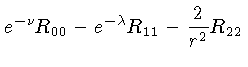
![$ e^{-\lambda}[-\nu^{\prime\prime} + \frac{1}{2}\lambda^\prime...
...r^2} +
\frac{2\lambda^\prime}{r} - \frac{2\nu^\prime}{r}] + \frac{2}{r^2}$](img3035.gif)