Mais energia de Fermi
O nosso objetivo é obter expressões para a Energia de Fermi para os seguintes
casos:
- um gás a temperatura zero
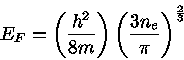 |
(1) |
- um gás não-degenerado e ionizado
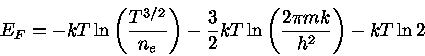 |
(2) |
- um gás fracamente degenerado;
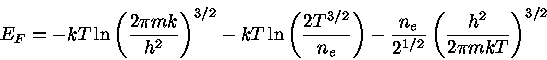 |
(3) |
- um gás altamente degenerado e ultra-relativístico.
![\frac{1}{E_{F}} = \frac{1}{E_{F}(T=0)}[ 1+\pi^2(\frac{kT}{E_{F}})^2 ]^{1/3}](img4.gif) |
(4) |
Para um gás em equilíbrio, a configuração mais provável depende da natureza
do gás. Temos as partículas:
1) idênticas, mas distingüíveis, que são partículas
clássicas;
2) idênticas, mas indistingüíveis de spin semi-inteiro e
3)
idênticas, mas indistingüíveis de spin inteiro.
Assim, para partículas clássicas, temos
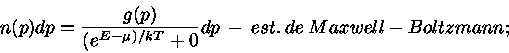 |
(5) |
para partículas quânticas como elétrons, pósitrons e neutrinos temos
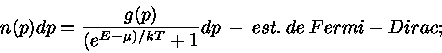 |
(6) |
para partículas quânticas como fótons, mésons  e partículas
e partículas  temos
temos
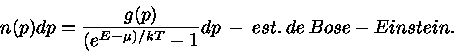 |
(7) |
Da termodinâmica,
sabemos que
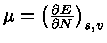 ,
onde
,
onde 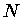 é a densidade total (número de partículas por unidade de volume),
sendo normalizado da seguinte forma:
é a densidade total (número de partículas por unidade de volume),
sendo normalizado da seguinte forma:
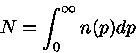 |
(8) |
Na Estatística de Fermi-Dirac,
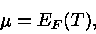 |
(9) |
onde 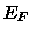 é chamada de energia de Fermi, dependendo fracamente da
temperatura.
é chamada de energia de Fermi, dependendo fracamente da
temperatura.
O fator de degenerescência pode ser obtido usando-se o princípio da
incerteza Heisenberg e fato de que para elétrons e para fótons podem existir
dois estados de polarização (spin), e que o volume do espaço de momentum,
para o qual o vetor 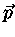 tem magnitude constante p, é simplesmente o
volume da casca esférica,
tem magnitude constante p, é simplesmente o
volume da casca esférica, 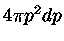 :
:
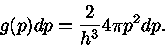 |
(10) |
Todas as partículas possuem energia 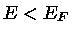 , estando os estados cuja
energia
, estando os estados cuja
energia 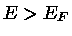 desocupados. Portanto, a partícula mais energética tem
momento
desocupados. Portanto, a partícula mais energética tem
momento 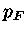 e a integral da equação (8) fica:
e a integral da equação (8) fica:
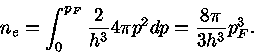 |
(11) |
Assim,
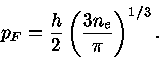 |
(12) |
A esta temperatura podemos considerar a velocidade não relativística (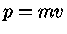 )
)
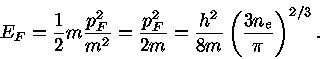 |
(13) |
Para um gás não degenerado e monoatômico com baixa densidade, as expressões
para 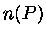 clássicas e quânticas devem ser iguais. A expressão clássica
para
clássicas e quânticas devem ser iguais. A expressão clássica
para 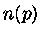 é
é
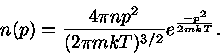 |
(14) |
Já a equação corresponde da mecânica quântica (com 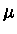 grande e negativo)
para
grande e negativo)
para 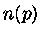 é
é
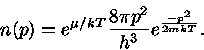 |
(15) |
Igualando as duas expressões acima, temos
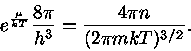 |
(16) |
Simplificando a expressão (16), podemos obter uma expressão para 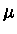
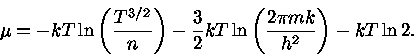 |
(17) |
Como
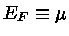 , então
, então
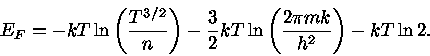 |
(18) |
Um gás de elétrons é descrito pela estatística de Fermi-Dirac. Assim, a
densidade de elétrons com momentum  entre
entre  e
e 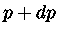 é dada por
é dada por
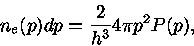 |
(19) |
onde 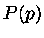 é definido como índice de ocupação para um de gás de Fermi.
é definido como índice de ocupação para um de gás de Fermi.
![P(p)=[ e^{\frac{E-\mu}{kT}} +1 ]^{-1} = \frac{1}{e^{\frac{E-\mu}{kT}}[1+e^{-\frac{E-\mu}{kT}}]}](img38.gif) |
(20) |
![P(p)\simeq e^{-\frac{E-\mu}{kT}} [ 1-e^{-\frac{E-\mu}{kT}}].](img39.gif) |
(21) |
Por conseqüência, temos
Utilizando a eq. (21) na eq. (19) e definindo
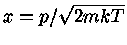 , com
, com
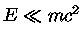 , obtemos
, obtemos
onde  é o potencial químico de um gás não-degenerado, dado pela eq.
(13).
é o potencial químico de um gás não-degenerado, dado pela eq.
(13).
Simplificando a eq. (24), obtemos:
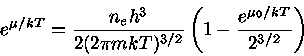 |
(25) |
![\mu=kT \ln [ \frac{n_{e} h^3}{2(2\pi mkT)^{3/2}} ( 1-\frac{e^{\mu_{0}/kT}}{2^{3/2}} ) ]](img51.gif) |
(26) |
![\mu=-kT \ln [ \frac{2(2\pi mkT)^{3/2}}{n_{e} h^3} ( 1-\frac{e^{\mu_{0}/kT}}{2^{3/2}} )^{-1} ]](img52.gif) |
(27) |
Mas
 , se
, se 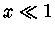 , então fazendo
, então fazendo
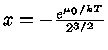
![\mu=-kT \ln [ \frac{2(2\pi mkT)^{3/2}}{n_{e} h^3} ( 1-\frac{e^{\mu_{0}/kT}}{2^{3/2}} )^{-1} ]](img52.gif) |
(28) |
utilizando a equação (16) para o termo em 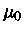 , obtemos:
, obtemos:
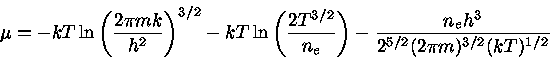 |
(29) |
Como
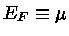 :
:
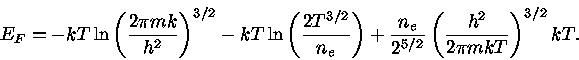 |
(30) |
Neste regime, 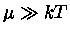 Temos que
Temos que
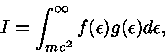 |
(31) |
onde 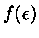 é a probabilidade que um particular estado de momentum esteja
ocupado.
é a probabilidade que um particular estado de momentum esteja
ocupado.
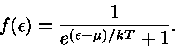 |
(32) |
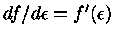 tem um máximo em
tem um máximo em
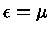 e é pequeno para valores de
e é pequeno para valores de 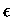 que são ou muito menores ou muito maiores
do que
que são ou muito menores ou muito maiores
do que 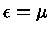 . As funções
. As funções 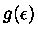 variam muito menos que
variam muito menos que 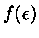 .
Integrando a eq. (32) por partes, temos
.
Integrando a eq. (32) por partes, temos
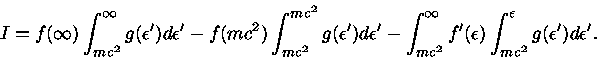 |
(33) |
Podemos definir
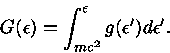 |
(34) |
A eq. (32) fica
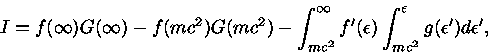 |
(35) |
mas 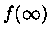 e
e 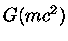 são zero.
são zero.
Logo, podemos escrever a eq. (32) como
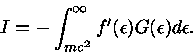 |
(36) |
Podemos, agora, definir
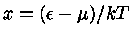 e expandir
e expandir 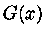 em séries de
Taylor para
em séries de
Taylor para 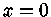 . Obtemos
. Obtemos
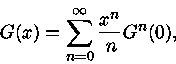 |
(37) |
com
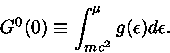 |
(38) |
Por outro lado,
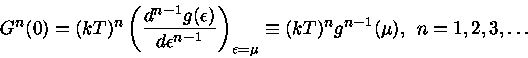 |
(39) |
Utilizando as eq. (38-40) na eq. (37), temos
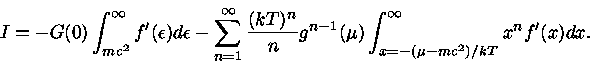 |
(40) |
Entretanto,
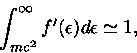 |
(41) |
pois 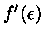 tem o comportamento semelhante ao da função Delta de Dirac
(em um gás fortemente degenerado), onde
tem o comportamento semelhante ao da função Delta de Dirac
(em um gás fortemente degenerado), onde
![f'(x) = -\frac{e^x}{kT [e^x +1]^2}=-\frac{1}{kT (e^x +1)(e^{-x} +1)}](img83.gif) |
(42) |
Podemos notar que 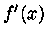 é uma função par. Como
é uma função par. Como 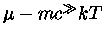 , podemos
analisar a integral do segundo termo da eq. (41) como tendo os limites
, podemos
analisar a integral do segundo termo da eq. (41) como tendo os limites 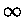 e
e 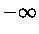 .
Desta forma, apenas valores pares de
.
Desta forma, apenas valores pares de 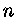 terão importância na integral
mencionada e, por conseqüência, apenas as derivadas ímpares da função
terão importância na integral
mencionada e, por conseqüência, apenas as derivadas ímpares da função
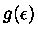 aparecerão na expressão final para
aparecerão na expressão final para 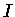 .
.
Como 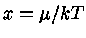 é positivo, então podemos escrever
é positivo, então podemos escrever
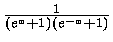 como a expansão binomial
como a expansão binomial
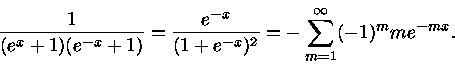 |
(43) |
Assim, a integral do segundo termo da eq. (41) se torna
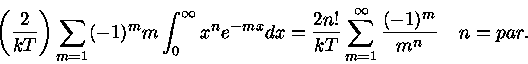 |
(44) |
Podemos, agora, escrever a eq. (32) como
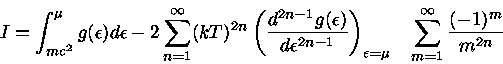 |
(45) |
ou então
Escrevendo uma expressão para a densidade de elétrons dada na eq.
(19) como função de 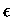 com
com
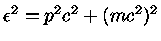 , obtemos
, obtemos
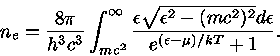 |
(47) |
A equação (48) implica que
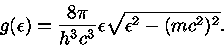 |
(48) |
A derivada de 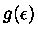 fica
fica
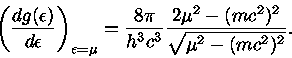 |
(49) |
Deste modo, usando as eq. (47-50) e considerando apenas os dois primeiros
termos do lado direito da eq. (47), obtemos
Para um gás não relativístico de elétrons podemos definir o potencial
químico 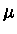 como
como
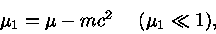 |
(51) |
manipulando a eq. (52), obtemos
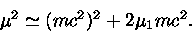 |
(52) |
Substituindo a expressão para 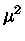 da eq. (52) na eq. (51) nos dá
da eq. (52) na eq. (51) nos dá
![n_{e}=\frac{32\pi (m\mu_{1})^{3/2}}{3\sqrt{2}h^3} [1+ \frac{\pi^2}{8} (\frac{kT}{\mu_{1}} )^2 ]](img109.gif) |
(53) |
Como
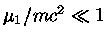 , a eq. (53) fica
, a eq. (53) fica
onde
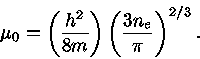 |
(55) |
Note-se que o potencial químico 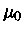 é a Energia de Fermi
é a Energia de Fermi 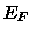 da expressão (13).
da expressão (13).
Como 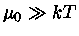 , então
, então
![\mu_{1}=\mu_{0} [ 1-\frac{\pi^2}{12} ( \frac{kT}{\mu_{0}})^2 ].](img116.gif) |
(56) |
Para um gás ultra-relativístico, 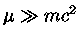 e a eq. (51) se torna
e a eq. (51) se torna
com
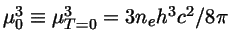 .
.
 Energia de Fermi
Energia de Fermi
 Evolução Estelar
Evolução Estelar
 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 15 março 2006
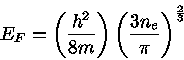
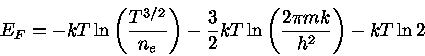
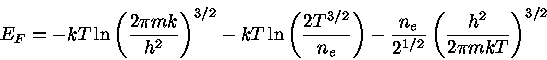
![\frac{1}{E_{F}} = \frac{1}{E_{F}(T=0)}[ 1+\pi^2(\frac{kT}{E_{F}})^2 ]^{1/3}](img4.gif)
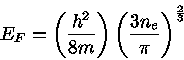
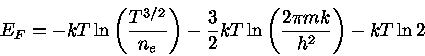
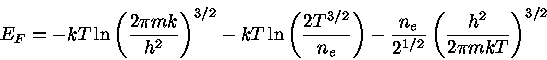
![\frac{1}{E_{F}} = \frac{1}{E_{F}(T=0)}[ 1+\pi^2(\frac{kT}{E_{F}})^2 ]^{1/3}](img4.gif)
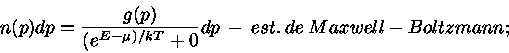
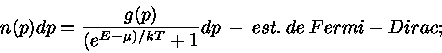
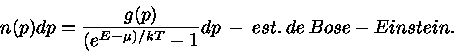
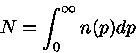
![]() tem magnitude constante p, é simplesmente o
volume da casca esférica,
tem magnitude constante p, é simplesmente o
volume da casca esférica, ![]() :
:
![]() , estando os estados cuja
energia
, estando os estados cuja
energia ![]() desocupados. Portanto, a partícula mais energética tem
momento
desocupados. Portanto, a partícula mais energética tem
momento ![]() e a integral da equação (8) fica:
e a integral da equação (8) fica:
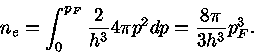
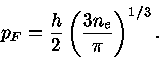
![]() )
)
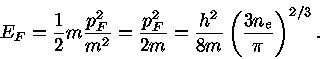
![]() clássicas e quânticas devem ser iguais. A expressão clássica
para
clássicas e quânticas devem ser iguais. A expressão clássica
para ![]() é
é
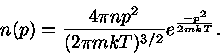
![]() grande e negativo)
para
grande e negativo)
para ![]() é
é
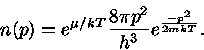
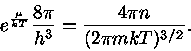
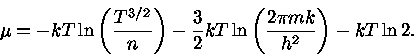
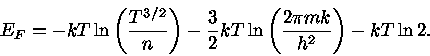
![]() entre
entre ![]() e
e ![]() é dada por
é dada por
![P(p)=[ e^{\frac{E-\mu}{kT}} +1 ]^{-1} = \frac{1}{e^{\frac{E-\mu}{kT}}[1+e^{-\frac{E-\mu}{kT}}]}](img38.gif)
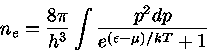
![$ \frac{8\pi (2mkT)^{3/2}}{h^3} [e^{\mu/kT} \int_{0}^{\infty}e^{-x^2}x^2dx- e^{2\mu /kT}\int_{0}^{\infty} e^{-2x^2}x^2 dx ]$](img45.gif)
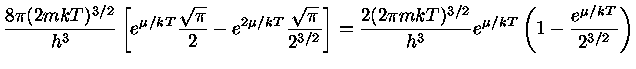
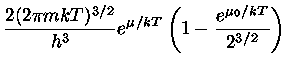
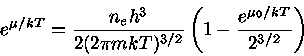
![\mu=kT \ln [ \frac{n_{e} h^3}{2(2\pi mkT)^{3/2}} ( 1-\frac{e^{\mu_{0}/kT}}{2^{3/2}} ) ]](img51.gif)
![\mu=-kT \ln [ \frac{2(2\pi mkT)^{3/2}}{n_{e} h^3} ( 1-\frac{e^{\mu_{0}/kT}}{2^{3/2}} )^{-1} ]](img52.gif)
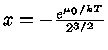
![\mu=-kT \ln [ \frac{2(2\pi mkT)^{3/2}}{n_{e} h^3} ( 1-\frac{e^{\mu_{0}/kT}}{2^{3/2}} )^{-1} ]](img52.gif)
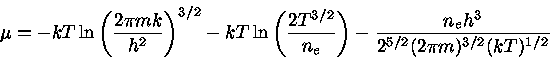
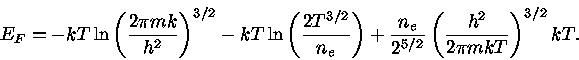
![]() Temos que
Temos que
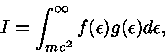
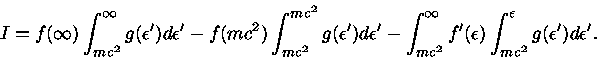
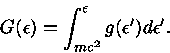
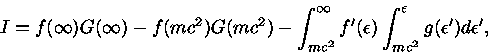
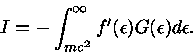
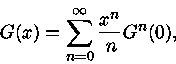
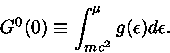
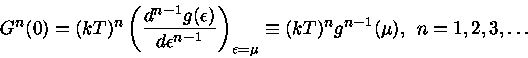
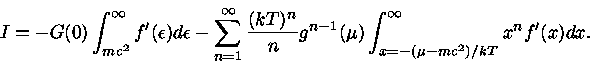
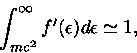
![f'(x) = -\frac{e^x}{kT [e^x +1]^2}=-\frac{1}{kT (e^x +1)(e^{-x} +1)}](img83.gif)
![]() é positivo, então podemos escrever
é positivo, então podemos escrever
![]() como a expansão binomial
como a expansão binomial
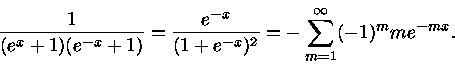
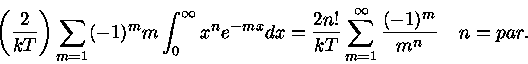
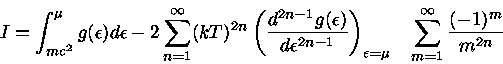
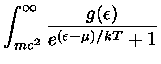
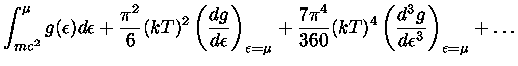
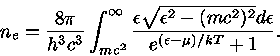
![]() fica
fica
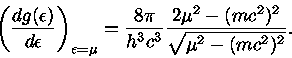
![$ \frac{8\pi}{h^3c^3} [ \int_{mc^2}^{\mu} \epsilon \sqrt{\epsi...
...^2}{6}(kT)^2
(\frac{2\mu^2-(mc^2)^2}{\sqrt{\mu^2-(mc^2)^2}}) ]$](img103.gif)
![$ \frac{8\pi}{h^3c^3} [ \frac{(\epsilon ^2-(mc^2)^2)^{3/2}}{3}...
...}{6} (kT)^2 (\frac{2\mu^2-(mc^2)^2}{\sqrt{\mu^2-(mc^2)^2}}
) ]$](img104.gif)
![$ \frac{8\pi}{h^3c^3} [ \frac{(\mu^2-(mc^2)^2)^{3/2}}{3} +
\fr...
...{6} (kT)^2 (\frac{2\mu^2-(mc^2)^2}{\sqrt{\mu^2-(mc^2)^2}}
) ].$](img105.gif)
![]() como
como
![]() da eq. (52) na eq. (51) nos dá
da eq. (52) na eq. (51) nos dá
![]() , a eq. (53) fica
, a eq. (53) fica
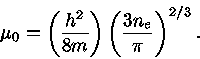
![]() , então
, então
![\mu_{1}=\mu_{0} [ 1-\frac{\pi^2}{12} ( \frac{kT}{\mu_{0}})^2 ].](img116.gif)
![$ \frac{1}{\mu_{0}^3}[1+\pi^2
(\frac{kT}{\mu})^2 ]$](img119.gif)
![$ \frac{1}{\mu_{0}^3}[1+\pi^2
(\frac{kT}{\mu_{0}})^2 ],$](img120.gif)
![]()